C Multi-task Token-level Regression for Gaze Metrics Prediction
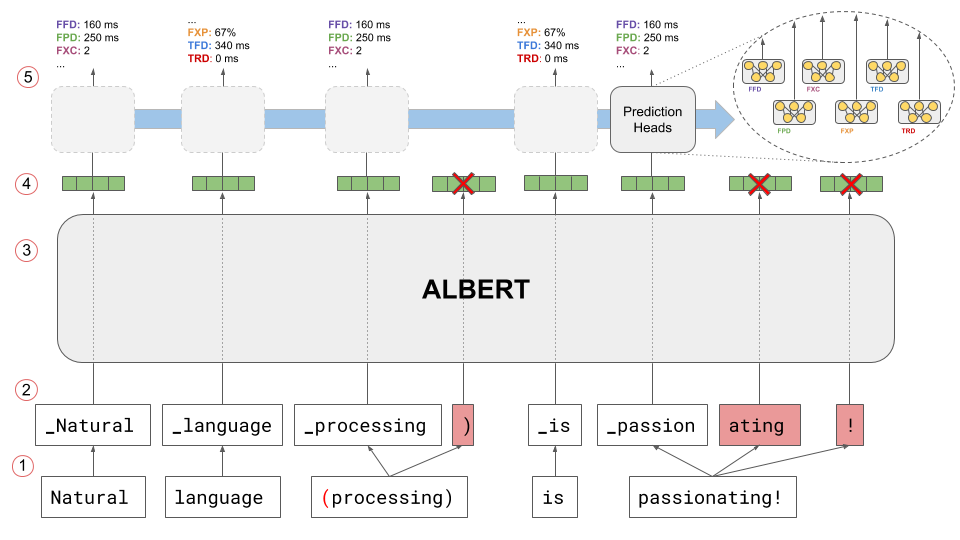
Figure C.1: Multi-task token-level regression on eye-tracking annotations. Preceding punctuation is removed (1), and the sentence is tokenized while keeping track of non-initial tokens (2). Embeddings are fed to the ALBERT model (3), and non-initial representations are masked to ensure a one-to-one mapping between labels and predictions (4). Finally, task-specific prediction heads are used to predict gaze metrics in a multitask setting with hard parameter sharing (5).
A multitask token-level regression fine-tuning approach was adopted throughout this study to predict eye-tracking metrics using neural language models. This novel approach’s choice stems from the fact that the regression task of predicting gaze metrics is inherently word-based given the granularity of eye-tracking annotations and that different gaze metrics provide complementary viewpoints over multiple stages of cognitive processing and can as such be modeled more precisely in a multitask learning setting. Figure C.1 presents the model’s training and inference procedure, closely matching other approaches used to train neural language models for sequence tagging tasks like POS tagging and named entity recognition.
The most defining detail in the procedure is the need to preserve an exact one-to-one mapping between input words and gaze metrics annotations, which is non-trivial in light of subword tokenization approaches that represent nowadays the de facto standard for training modern neural language models. To enforce such mapping, two steps are taken. First, all initial punctuation (e.g. the open parenthesis before processing in Figure C.1 example) is removed to make the initial subword token for that word (i.e. the one preceded by whitespace) equal to the word’s first characters. Then, all non-initial subword tokens are identified in step (2), and their respective embeddings are masked in step (4) before passing the remaining initial embeddings (one per whitespace-tokenized word at this point, as for gaze metrics) to the set of prediction heads responsible for inferring individual gaze metrics. While this procedure can be regarded as suboptimal since not all learned representations are used for prediction, it is essential to remember that all the embeddings produced by attention-based neural language models are contextualized and encode information about the entire sentence and surrounding context to some extent. In this sense, initial token embeddings can be trained in this setting to predict gaze metrics relative to the whole word, effectively bypassing the issues about information loss raised by the masking procedure.
Another important detail in the training and inference procedure is the standardization of metrics, which plays a key role in this setup due to the different ranges of different metrics (e.g. fixation probability is always defined in the interval \([0,1]\), while gaze durations are integers in the scale of hundreds/thousands of milliseconds). Specifically, considering the set \(X\) of values assumed by a specific metric for all tokens in the eye-tracking datasets, the average \(\mu_X\) and standard deviation \(\sigma_X\) of those values are computed, and each value is transformed as: \[\begin{equation} X_i' = \frac{X_i - \mu_X}{\sigma_X} \end{equation}\] to produce a new range \(X'\) with average equal to \(0\) and standard deviation equal to \(1\). Predicted values are then reconverted to the original scale as \(X_i = (X'_i \cdot \sigma_X) + \mu_X\) when performing inference, and training and testing metrics are computed on each metric’s original scale.
Spillover concatenation Cognitive processing literature reports evidence of reading times for a word being shaped not only by the predictability of the word itself but also by the predictability of the words that precede it (Smith and Levy 2013) in what is commonly referred to as the spillover effect (Mitchell 1984). The existence of spillover has important implications in the context of this gaze metrics prediction approach since the embeddings for a single word may not contain enough information to predict the influence of preceding tokens in shaping reading behaviors. Notably, Schijndel and Linzen (2020) include the surprisal of the three previous words in a mixed-effect model used to estimate a surprisal-to-reading-times conversion coefficient. While it can be hypothesized that in this approach, the usage of contextualized word embeddings can automatically account for this type of interaction, the effect of leveraging preceding tokens for the current token’s metric prediction is assessed to confirm this hypothesis. A new procedure defined as spillover concatenation is introduced for this purpose, in which token embeddings are augmented by performing a rolling concatenation of the \(n\) preceding embeddings before feeding the final representation to prediction heads. Initial tokens are padded with \(0\) vectors to match the fixed size defined by embedding size and the \(n\) parameter. For example, using spillover concatenation with \(n = 3\) within a BERT model with a hidden size of 768 involves having prediction heads taking input size of \(768 \cdot (3 + 1) = 3072\), the size of the token embedding for which gaze metrics should be predicted plus the size of the three preceding token embeddings. In this way, information about preceding tokens is explicitly included at prediction time.
Figure C.2 shows the validation losses during training for the two models used in the experiments of Chapter 5 with their counterparts using spillover concatenation. Model performances are not positively influenced by introducing the concatenation technique and remain very similar for both architectures.
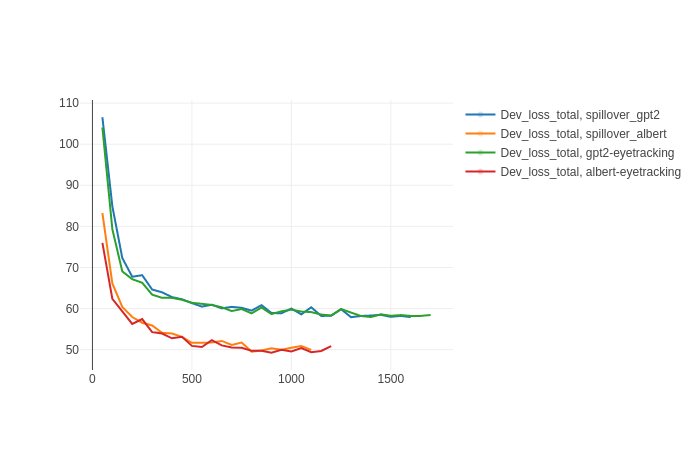
Figure C.2: Validation total loss for GPT-2 and ALBERT over a split of the eye-tracking merged corpora with and without spillover concatenation. Model predictive performances were comparable across training and testing for the two models.
Model performances Table C.1 presents the test performances of ALBERT and GPT-2 models trained with and without the spillover concatenation approach on the merge of all eye-tracking corpora. The top two rows present descriptive statistics about extreme values, the mean and standard deviation in annotations averaged across participants for each metric. It is interesting to observe that the maximum value observed for first pass duration (FPD) is higher than the one for total fixation duration (TFD). While this situation would not be possible in practice due to first pass duration being included in total reading times, it reminds us about the approximate nature of our filling-and-averaging procedure described in Appendix B. Comparing results to those of Table 3.2, where gaze metrics were modeled at the sentence level, we observe much worse results in terms of explained variance for both models: while fixations and first pass duration (FXC, FXP, FPD) are generally well modeled, worse results are obtained for first and total fixation durations (FFD, TFD), and in particular for the duration of regression (TRD). These results can be attributed to the merging of different corpora that, being annotated by different participants, present very different properties, as shown in Table 1.4 and Figure 5.2. While on the one hand, this choice harms modeling performances, on the other hand, it provides us with more representative results for the general setting.
| FFD | FPD | FXP | FXC | TFD | TRD | |
|---|---|---|---|---|---|---|
| min-max value | \(0-986\) | \(0-2327\) | \(0-1\) | \(0-8.18\) | \(0-1804\) | \(0-4055\) |
| \(\mu|\sigma\) statistics | \(162|50\) | \(188|86\) | \(.56|.27\) | \(.85|.53\) | \(206|87\) | \(90|122\) |
| ALBERT | \(41_{78}|.33\) | \(61_{121}|.50\) | \(.17_{.32}|.60\) | \(.31_{.62}|.66\) | \(65_{132}|.44\) | \(110_{207}|.19\) |
| ALBERT Spillover | \(41_{78}|.33\) | \(61_{122}|.50\) | \(.17_{.33}|.60\) | \(.31_{.62}|.66\) | \(65_{132}|.44\) | \(110_{208}|.19\) |
| GPT-2 | \(44_{83}|.23\) | \(68_{136}|.37\) | \(.18_{.35}|.56\) | \(.36_{.70}|.54\) | \(74_{149}|.28\) | \(115_{222}|.11\) |
| GPT-2 Spillover | \(43_{83}|.26\) | \(68_{135}|.37\) | \(.19_{.35}|.50\) | \(.36_{.70}|.54\) | \(73_{146}|.30\) | \(116_{220}|.10\) |
In general, better performances are observed for the masked language model ALBERT, suggesting the importance of having access to bidirectional context for gaze metrics prediction. Results present additional evidence supporting the superfluity of the spillover concatenation procedure, which was henceforth dropped in the context of Chapters 4 and 5’s experiments. Although good scores in terms of average and maximal errors are observed for all metrics, the relatively low \(R^2\) seem to suggest that large margins of improvement are still available in the context of gaze metrics predictions with neural language models.
References
Mitchell, Don C. 1984. “An Evaluation of Subject-Paced Reading Tasks and Other Methods for Investigating Immediate Processes in Reading.” New Methods in Reading Comprehension Research, 69–89.
Schijndel, Marten van, and Tal Linzen. 2020. “Single-Stage Prediction Models Do Not Explain the Magnitude of Syntactic Disambiguation Difficulty.” PsyArXiv Pre-Print sgbqy. https://psyarxiv.com/sgbqy/.
Smith, Nathaniel J, and Roger Levy. 2013. “The Effect of Word Predictability on Reading Time Is Logarithmic.” Cognition 128 (3). Elsevier: 302–19.